生成对抗式网络(Generative Adversarial Networks)

在近期深度学习技术的各项突破中有一个非常有趣的研究工作，叫做生成对抗式网络：Generative Adversarial Networks（以下简称GAN），最开始由Bengio所在实验室的人提出^[1]，然后被其他人做了一些改进，应用到一些更大的数据上后并做了进一步的拓展分析。

模型介绍

与一般的被用于Supervised Learning任务的深度神经网络不同，GAN同时要训练一个生成网络(Generator)和一个判别网络(Discriminator)，前者输入一个noise变量 \(z\) ，输出一个伪图片数据 \(G(z; \theta_g)\) ，后者输入一个图片(real image)／伪图片(fake image)数据 \(x\) ，输出一个表示该输入是自然图片或者伪造图片的二分类置信度 \(D(x;\theta_d)\) ，理想情况下，判别器 \(D\) 需要尽可能准确的判断输入数据到底是一个真实的图片还是某种伪造的图片，而生成器G又需要尽最大可能去欺骗D，让D把自己产生的伪造图片全部判断成真实的图片。

根据上述训练过程的描述，我们可以定义一个损失函数：

\[\text{Loss} = \frac{1}{m}\sum_{i=1}^m[\log D(x^i) + log(1-D(G(z^i)))]\]

其中 \(x^i, z^i\) 分别是真实的图片数据以及noise变量。

而优化目标则是：

\[\min_G\max_D \text{Loss}\]

不过需要注意的一点是，实际训练过程中并不是直接在上述优化目标上对 \(\theta_d, \theta_g\) 计算梯度，而是分成几个步骤：

训练判别器即更新 \(\theta_d\) ：循环k次，每次准备一组real image数据 \(x={x^1, x^2, \cdots, x^m}\) 和一组fake image数据 \(z={z^1, z^2, \cdots, z^m}\) ，计算 \(\nabla_{\theta_d}\frac{1}{m}\sum_{i=1}^m[\log D(x^i) + log(1-D(G(z^i)))]\) 然后梯度上升法更新

$$\theta_d$$ ；    2. 训练生成器即更新 $$\theta_g$$ ：准备一组fake image数据 $$z={z^1, z^2, \cdots, z^m}$$ ，计算
  $$\nabla_{\theta_g}\frac{1}{m}\sum_{i=1}^mlog(1-D(G(z^i)))$$
然后梯度下降法更新 

$$\theta_g$$ 。 

可以看出，第一步内部有一个k层的循环，某种程度上可以认为是因为我们的训练首先要保证判别器足够好然后才能开始训练生成器，否则对应的生成器也没有什么作用，然后第二步求提督时只计算fake image那部分数据，这是因为real image不由生成器产生，因此对应的梯度为0。

训练细节

上节主要内容来自GAN被提出时的那片论文，但是后来人们在进行实践时发现这个训练方法虽然听上去非常美好，两个网络相互对抗，共同促进，但是实际跑起来的时候却非常不理想，很难收敛，于是Radford等人在2015年总结了一下自己的实验经验，挂了一篇文章^[2]在arXiv上，里面有提到几个非常关键的模型训练要点：

把判别器D中的所有Pooling层更换成strided convolutions，把生成器G中的所有Pooling层换成fractional-strided convolutions（或者叫做deconvolution层，虽然作者觉得这种叫法是非常蠢的错误叫法?）；
同时在判别器和生成器中使用Batch Normalization；
不要使用全连接层；
生成器中除了输出那层用tanh作为激活函数，其他都用ReLU；
判别器中所有激活函数都用Leaky ReLU。

虽然作者也不能明明白白的说出每一点的理由，不过考虑到这些也是经过无数个夜晚试出来的人生经验，还是暂且相信了吧。

下图是论文^[2]中生成器的网络结构图，

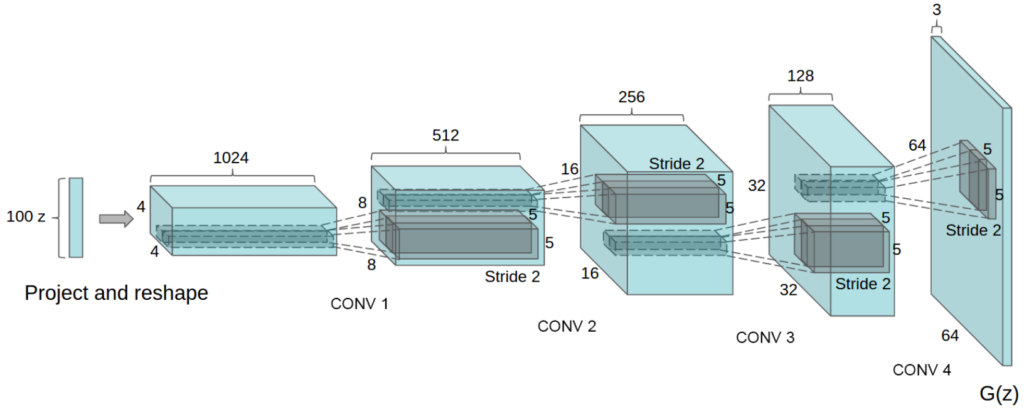
基本可以认为就是一个正常的CNN分类网络反过来的结构，例如假设输入的rand是batch=100, channel=200, height=1, width=1的随机数，那么经过一个kernel=(4, 4), num_filter=512的fractional-strided convolution后，就变成了(100, 512, 4, 4)的矩阵，然后越往后长、宽越大，通道数越小，最后变成一个3*64*64的fake image。

代码分析

关于论文^[2]在很多深度学习库上都能找到对应的实现，这里以MXNet为例进行介绍，详细的代码文件请点这里（另外，这份样例代码与大神陈天奇编写的版本非常相似，不知是本人修改过来的还是怎样，反正如果只关注GAN算法的话，使用mxnet官方的这份代码完全足够，结构也很清晰易懂。）

打开代码文件后可以看到除了main函数之外，还有make_dcgan_sym、get_mnist、fill_buf、visual四个函数，分别用于生成判别器、生成器的网络结构，获取mnist数据，把多个小图填充到一个大图(buf)中，可视化显示，然后RandIter和ImagenetIter分别是产生noise data和ImageNet real image的DataIter，当然如果使用的是mnist数据，后面那个数据迭代器也不需要关注。

实际训练的参数设置与代码都在main函数里，仔细比对了一遍，该代码主要是在训练判别器的地方与论文有些出入，并没有循环k次，而是每个iteration中G和D都只更新一次，主要的训练代码如下：

for epoch in range(100):
        train_iter.reset()
        for t, batch in enumerate(train_iter):
            rbatch = rand_iter.next()

            modG.forward(rbatch, is_train=True)
            outG = modG.get_outputs()

            # update discriminator on fake
            label[:] = 0
            modD.forward(mx.io.DataBatch(outG, [label]), is_train=True)
            modD.backward()
            gradD = [[grad.copyto(grad.context) for grad in grads] for grads in modD._exec_group.grad_arrays]

            # update discriminator on real
            label[:] = 1
            batch.label = [label]
            modD.forward(batch, is_train=True)
            modD.backward()
            for gradsr, gradsf in zip(modD._exec_group.grad_arrays, gradD):
                for gradr, gradf in zip(gradsr, gradsf):
                    gradr += gradf
            modD.update()

            # update generator
            label[:] = 1
            modD.forward(mx.io.DataBatch(outG, [label]), is_train=True)
            modD.backward()
            diffD = modD.get_input_grads()
            modG.backward(diffD)
            modG.update()

            mG.update([label], modD.get_outputs())

不过在最初看这段代码时有两个关于参数更新的疑问：

优化目标是通过G最小化Loss，通过D最大化Loss，那么在更新D时利用梯度上升，更新G时应该利用梯度下降，也就是G需要获取D输入处的负梯度（比如G在后向传播阶段是不是可以改成modG.backward(-diffD)？），为什么代码中完全没有体现，非常简单的forward、backward然后update了？
更新G时，由G产生fake image的label为什么被设置成1（26行label[:] = 1）？

个人觉得可以从两个角度进行理解：

1.感性上，如果我们把这个label设置成1，那么产生的梯度就会逐渐让网络把输入的数据类型判断成正样本，也就达到了欺骗判别器的目的；

2.数学上，在论文中有这么一段话：

“Early in learning, when G is poor, D can reject samples with high confidence because they are clearly different from the training data. In this case, \(\log (1-D(G(z)))\) saturates. Rather than training G to minimize \(\log (1-D(G(z))\) we can train G to maximize log \(D(G(z))\) . This objective function results in the same fixed point of the dynamics of G and D but provides much stronger gradients early in learning.”

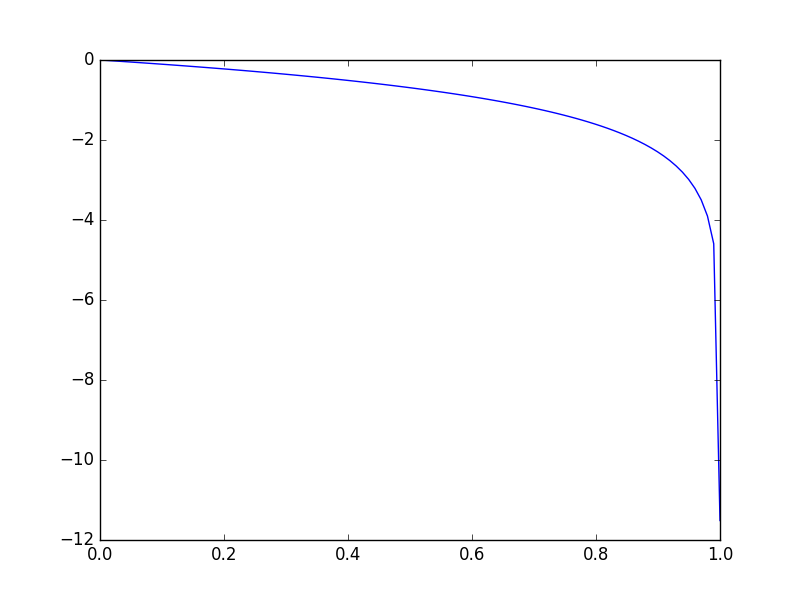
因为 \(\log(1-D(G(z)))\) 在早期的时候由于D判断的非常准，因此预测出的 \(D(G(z))\) 基本都是0，而 \(\log(1-x)\) 函数如下图所示，在x接近0的地方梯度也非常小，使得模型每次更新收敛速度非常慢，因此与其最小化这个不如直接最大化 \(\log D(G(z))\) ，新的优化函数不管x接近0还是1，都能保持比较大的梯度，并且这样变换后，相当于两次都是使用正常的梯度上升，中间梯度不需要变换符号，只需要改变label从0到1，使得被保留的梯度只包含Loss函数求和项的第一部分，一举两得。

［1］ Goodfellow, Ian, et al. “Generative adversarial nets.” Advances in Neural Information Processing Systems. 2014.

［2］ Radford, Alec, Luke Metz, and Soumith Chintala. “Unsupervised representation learning with deep convolutional generative adversarial networks.” arXiv preprint arXiv:1511.06434 (2015).

模型介绍

训练细节

代码分析

nicklhy