本文是对Michael Jordan关于Probability Graph Model的一篇tutorial(http://www.cis.upenn.edu/~mkearns/papers/barbados/jordan-tut.pdf)的细节补充。

首先，图模型（Graph Model）分为两种类型：有向图（Directed Graph）和无向图（Undirected Graph）。我们平时接触到的belief networks, bayesian networks, probabilistic

independence networks, Markov random fields, loglinear models, influence diagrams等很多模型也都属于概率图模型的范畴，下面从基本概念开始介绍：

1.Directed Graph

一般在PGM中提到有向图是指有向无环图，图中的结点也不需要人工去分类成“输入”、“输出”、“隐藏结点”等。

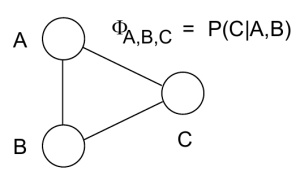
Define: Random variable \(X\) is marginal independent of random variable \(Y\) if, for all \(x_i \in dom(X), y_k \in dom(Y)\) , we have

Define: Random variable \(X\) is conditionally independent of random variable \(Y\) given random variable \(Z\) if, for all  \(x_i \in dom(X), y_k \in dom(Y), z_m \in dom(Z)\) , we have

\(P(X=x_i|Y=y_k, Z=z_m) = P(X=x_i, Z=z_m)\) </span>

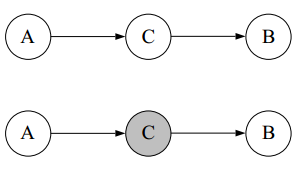
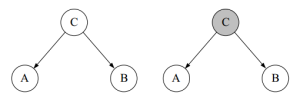
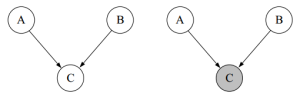上图中，前面A->C->B和C->A且C->B两种情况里，AB为marginally dependent，conditionally independent（给定观测值A或者B，会影响B或A的概率，但是若给定观测值C，则A或B的观测值不会影响B或A的概率），而最后一种A->C且B->C则正好相反，AB为marginally independent，conditionally dependent（给定A或B不影响B或A的概率，但是若给定观测值C，则A或B的观测值会影响B或A的概率）。

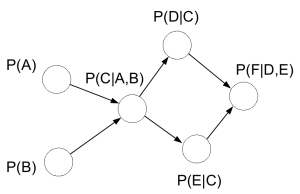在有向图中，如果我们用 \(S\) 表示所有结点的集合，用 \(pa(S_i)\) 表示结点 \(S_i\) 的所有父节点，那么整个结点集合的联合分布可以表示成：

并且可以证明，如果一个任意的概率分布满足上式，那么这个概率分布满足上面提到的conditional independence关系。

2.Undirected Graph

相对与有向图而言，无向图的情况会有比较大的差异。

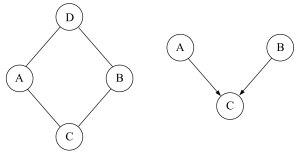上图是Michael的tutorial中一幅图片，并且图下注明说”The graph on the left yields conditional independencies that a directed graph can’t represent”, “ The graph on the right yields marginal independencies that an undirected graph can’t represent“，第一次看到这里不太明白，后来想了一会才懂，左边的无向图，ABCD四个随机变量如果给定AB或CD，则CD或AB条件独立，这种特殊情况在有向无环图中是不可能出现的（除非强行把ABCD的四条连接边变成双向边，但这样也就不符合标准有向图的定义了）；右边的有向图，AB因为没有公共父节点，因此二者满足marginal independence，如果换成无向图，由于边无向，能量可以双向传播，所以只要AB连通，就不可能满足marginal independence，但如果不连通，那么它们两个结点就不可能共同影响另外一个结点的条件概率。

在对无向图进行分析时，我们一般会以图中的团(clique)为单位入手：

找出其中的强连通分量，然后可以构成一个新的图

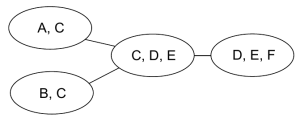现在我们对每一个团定义一个potential function，

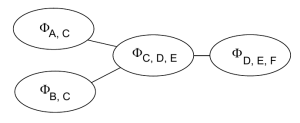那么在做过potential function的归一化之后，整个图的概率密度可以通过以下公式计算：

类似于有向图，我们也可以证明如果某个概率分布满足上式，那么这个概率分布的随机变量必然也满足conditional independence（这次居然是个有名字的定理，Hammersley-Cliord theorem）。

不过等等，不就是求个概率分布吗，为什么要把图分解成团？这个在Michael的tutorial里没有介绍，在google了之后，发现最根本的原因就是降低计算复杂度，或者用某书中的一句话：“概率图模型的核心就是图分解（factorization）”，想象如果不分解成团，正常的做法就是通过积分，把不需要的随机变量用贝叶斯那一套公式把每个结点所有状态累加一遍，但是这样有个问题，就是计算复杂度随着结点数量增加而指数级增长，所以在对付大规模图的时候就完全没法使用了。如果我们把图分成一个一个的满足conditional dependence的团，然后求取团块的概率，最终再把团块的概率综合起来求取整个网络的概率，复杂度就能大大的降低变成小区域的指数增长。

3.玻尔兹曼机（Boltzmann machine）

玻尔兹曼机其实是一种特殊的无向图模型，它的potential函数定义成 \(exp\{J_{ij}S_iS_j\}\) ，其中 \(J_{ij}\) 在i、j不相邻时等于0，potential函数本身既有能量的含义也有概率的意思。

4.Inference

Inference的意思就是求边缘分布。

4.1.Inference of Directed Graph Model

有很多用来inference有向图的方法，有些可以直接使用，但是tutorial里介绍的是一种需要先把DGM转换成UGM的叫做”junction tree”的算法，在介绍这个算法之前，还需要一点预备知识。

首先考虑一种特殊情形，A->C<-B

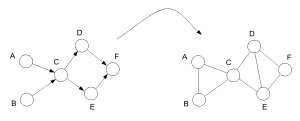
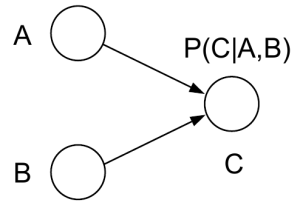如果我们要把一个有向图转换成一个无向图，最简单的方法就是把方向去掉，把边保留，不过在上面这种情况中会有一个问题，就是转换完了以后，ABC三个结点不在一个clique内，导致AC和BC两个团不满足原本有向图所包含的conditional independence properties，moralize就是一个比较简单的解决方案：如果两个结点具有公共的子节点，则在把有向边变成无向边之外，添加一条连接这两个结点的无向边。

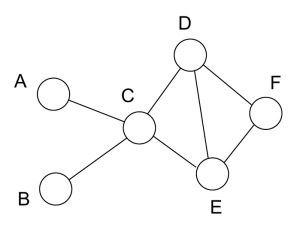
最终需要实现的就是把整个网络的inference任务变成各个clique子网络potential函数乘积，例如某个有向图的概率为：

在经过moralize之后，定义potential函数：

此时

有时候两个clique可能会包含相同的结点，理论上来说通过这两个团任意一个计算出的公共结点的联合概率应该也相同，但非常不幸，普通的图在定义potential函数之后不一定能够满足这种局部与全局的统一，于是我们需要采取一步特殊处理，Triangulation。

We say a cycle in G is chordless is all pairs of vertices that are not adjacent in the cycle are not neighbors.

A graph is triangulated if it contains no chordless cycles of length greater than 3.

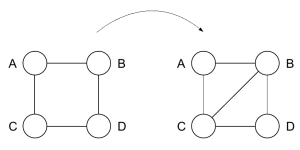这样的triangulated graph满足running intersection property: if a node appears in two cliques, it appears everywhere on the path between the cliques， 此时整个网络不管在局部的某个团内还是整体范围计算出的概率都能保持一致（consistency）。

对于这种triangulated graph的clique tree，还有一种特殊的称呼，Junction Tree，并且已经证明，仅有这种triangulated graph的clique tree满足running intersection property，能够保证local和global的consistency。