最后一周的笔记迟迟没有上，真是拖延症，课程其实已经结束，由于没有认证，所以和之前机器学习一样都是没有认证序列号的。
这次课的内容仍然与strategic相关，但与之前的情形有一些差异，从一个特殊的基本情况开始：
1.Start with a Canonical Special Case
- Each player chooses action \(x_i\) in {0,1}
- payoff will depend on: 1.how many neighbors choose each action. 2. how many neighbors a player has
也就是说，每个人的收益不再只受选择影响，还要考虑周围邻居以及他们做出的选择，也就是说，收益 \(u_{d_i}(x_i, m_{N_i})\) 是i结点度数 \(d_i\) 、选择 \(x_i\) 以及邻居中选择1的概率 \(m_{N_i}\) ，显然对收益函数不同的定义方式会导致网络中各个结点的不同决策分布，例如：
- Payoff action 0: \(u_{d_i} ( 0 ,m_{N_i} ) = 0\)
- Payoff action 1: \(u_{d_i} ( 1 ,m_{N_i})= -t + m_{N_i}\)
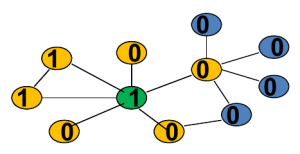
那么当且仅当一个结点周围有超过t比例的邻居选择了1，那么他也会选择1，否则选择0，类似于下图：
或者另一种极端情况：
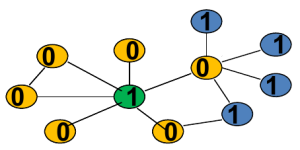
- Payoff action 0: \(u_{d_i}(0, m_{N_i})=1\) if \(m_{N_i}> 0\) , \(= 0\) if \(m_{N_i}\)
- Payoff action 1: \(u_{d_i} (1, m_{N_i} ) = 1-c\)
此时任意一个结点只有在周围没有邻居选择1的情况下才会选择1（就是这么高冷，逼格高。。。）：
2.Complements/Substitutes
上一小节说到不同的收益函数会导致结点做出不同的选择方案，这里我们尝试一下是否能把这些收益函数根据一些特性做个归纳。
第一个例子中，选择1的条件是某结点周围必须有足够多的邻居也选择了1（可以看成现实世界中随大流的人群，比如隔壁小花、小明考了一百分，你妈也要求你去考一百分）；而第二个例子完全不同，某结点选择1一定要周围没有其他人选择过1（就是这么任性，即使与全世界为敌我也不怕）。好的，那么具体决定两者不同的地方在哪里？呵呵，简单说来，其实就是收益函数u与周围邻居选择1的比例 \(m_i\) 成正相关还是负相关：
- strategic complements: for all \(d,m\ge m'\) , we have \(u_d(1,m)-u_d(0,m)\gt u_d(1,m')-u_d(0,m')\)
- strategic substitutes: for all \(d,m\ge m'\) , we have \(u_d(1,m)-u_d(0,m)\le u_d(1,m')-u_d(0,m')\)
说穿了，这其实就是判断 \(u_d(1,m)-u_d(0,m)\) 单调递增还是递减，如果是前者，如果周围朋友选择1的比例越多，我能得到的收益也就越大，相反，则越少。
3.Equilibrium
这个概念与前几节课出现时的定义相同：
Nash equilibrium: Every player’s action is optimal for that player given the actions of others.
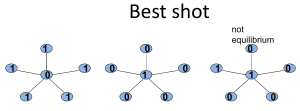上图前两种情况都属于Nash equilibrium，第三者因为左上那个结点为选择1，所以中间结点没有做出最优选择。
另外，一个网络可能存在多种equilibrium方案。
4.Maximal Independent Set
Independent Set: a set S of nodes such that no two nodes in S are linked;
Maximal: every node in N is either in S or linked to a node in S.
这是一个集合的概念，其中Independent是指集合S中任意两个结点都没有边直接相连，而Maximal则是指整个网络中所有结点要么属于S，要么与S中某个结点相连。
5.Complete lattice
Complete Lattice: for every set of equilibria X
- there exists an equilibrium x’ such that x’≥x for all x in X, and
- there exists an equilibrium x’‘ such that x’‘≤x for all x in X.
关于这个概念，不知道是不是理解错了，总觉得像一句废话。。。因为上面x’>=x和x’’<=x，如果可以取等号，那这个Complete Lattice性质显然是一定满足的，你不可能找到一个集合使得和它相等的另一个集合与它不想等（我特么在说什么。。。）
6.Beyond 0‐1 choices
上面逗比的一小节暂时忽略，考虑一下如何把之前0,1两种离散的选择拓展到[0,1]连续区间的情况，仍然先考虑简单的情形，收益函数为 \(f(x_i+\sum_{j\text{ in }N_i}x_j)-cx_i\) ，并且是一个凹函数（concave），如果 \(x^*>0\) 是最优解，也就是最大化收益函数，使得 \(f'(x^*)-c=0\) ，那么对于所有满足pure strategy Nash equilibria的情形，有：
\[x_i+\sum_{j \text{ in }N_i}x_j \ge x^*, \text{for all i, and if >, then } x_i=0\]然后equilibria又可以分两种情况：
- distributed: \(x^*>x_i > 0\) for some i’s
- specialized: for each i either \(x_i=0\) or \(x_i=x^*\)
前者 \(x_i\) 取值可以是0到 \(x^*\) 中的任意值，而后者要么相等，要么是0。
另外在specialized这种情况下，specialists( \(x^*=x_i\) )集合正好也是一个maximal independent集合。
