第一节课主要是对网络（图）模型进行一些基本定义的介绍，而这节课将会涉及到一些描述网络特性的概念。
1.Homophily
好吧，这单词不太清楚中文到底该怎么翻译（google translate直译出来是同质性），但其表达的意思很清楚，即一个大的社会网络中会存在许多小的子网络，而且原网络的大部分边都分布在各个子网络内部，而跨越两个不同子网络的边会比较少，比如一个高中里所有学生的好友关系网络，一般而言，每个年级内部不同学生之间存在好友关系的概率会远大于不同年级两个学生存在好友关系的概率，然后每个班级内部的好友关系密度又会大于同年级不同班级的好友关系密度。
Community Detection就是一种检测这种dense子网络的技术，不过这节课还没有涉及到，这里不再展开。
2.Centrality Measure
Centrality Measure是这次课的重点，用来描述网络中某个节点中心集中度，主要包括Degree、Closeness、Decay和Betweenness四种度量方式，并且每种方式的侧重点均不相同：
(a)Degree Centrality: 正如其名，Degree Centrality就是非常简单直接的统计每个节点的度数，如果一个节点的度数越高，那么其中心集中度也就越高，如果把每个节点的度数除以(n-1)，即可得到Normalized Degree Centrality。
不过Degree Centrality有一个很致命的缺点：它只能度量和某个节点直接相连的节点，而间接相连的将无法计算。举个例子，在Influence网络中，如果Ａ能影响10个人，这10个人每个都不能再影响其他人，而另外一个人B也能影响10个人，这10个人每人可以继续影响100人，这种情况下，如果用Degree Centrality来度量的话，A和B的影响力将会是等价的，但事实显然并非如此。
(b)Closeness Centrality:如果说上面的Degree Centrality描述的是节点connectedness程度，那么Closeness Centrality描述的则是某个节点到达其他所有节点的难易程度，定义如下：
\[\text{Closeness Centrality} = \frac{n-1}{\sum_j\mathcal{l}(i, j)}\]其中 \(l(i, j)\) 是节点i、j之间的距离。
(c)Decay Centrality: Decay Centrality和Closeness Centrality类似，目的都是描述某个节点与其他所有节点的综合距离，但不同点在于其并非简单的把这些距离相加然后取倒数，而是以指数的形式进行计算：
\[\text{Decay Centrality} = \sum_{j\not =?i}\delta^{l(i, j)}\]其中 \(\delta \in (0, 1)\) ，并且当 \(\delta\rightarrow?0\) 时，Decay Centrality变成Degree Centrality，当 \(\delta\rightarrow 1\) 时，变成该连通分量的size。
如果需要进行normalize，则：
\[\text{Normalized Decay Centrality} = \frac{\sum_{j\not =?i}\delta^{l(i, j)} }{(n-1)\delta}\](d)Betweenness Centrality: Betweenness Centrality很有意思，与前两种度量方式相比，它并不仅仅关注某个节点i到其他节点的距离，而是计算该节点在整个网络所有最短路径中的重要程度，定义为：
\[\text{Betweenness Centrality} = \frac{\sum_{i,j\not = k}[P_k(i, j)/P(i, j)]}{(n-1)(n-2)/2}\]这里 \(P(i, j)\) 表示节点i、j之间最短路径的数量，而 \(P_k(i, j)\) 则是在此基础上加上“k必须存在于这些路径上”的条件，也就是i、j之间最短且经过k的路径的数量。可以看出Betweenness Centrality测量的是某个节点在其他节点连通性中的重要性，如果在网络中删除某个节点，会导致很多其他节点的最短路径增加，则该节点的Betweenness Centrality越大，反之则越小。
(e)Eigenvector Measures: “Not what you know, but who you know.”
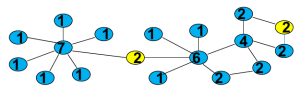上图中两个黄色节点的度数都是2，但是显而易见，中间的节点要比右边节点的中心集中度高很多，如果使用前面说的Closeness Centrality、Decay Centrality和Betweenness Centrality则可以区分出这两者的差别，Closeness Centrality和Decay是从该节点到其他所有节点的距离来度量，而Betweenness Centrality则是从该节点的通过性重要程度来度量，那么有没有可能从其他角度进行分析呢？Eigenvector Measures就是一个区别于前面集中方法的方式，原理上很直接，如果一个人认识了一些大人物，那么他很可能也是一个大人物～～
这里g是网络的邻接矩阵， \(g_{ij}\) 是边ij的权重，可以看到，等式左右的 \(C_i, C_j\) 都是未知数，如果写成矩阵的形式：
\[C = agC\]这里 \(C\in R^n\) 且 \(g \in R^{n\times n}\) ，a是矩阵g最大的特征值（根据Perron-Forbenius定理，该特征值大于0）。
上式显而易见，是一个标准的特征向量方程，这也是Eigenvector Measures名字的由来，另外，上式是否看起来很像之前一篇文章里介绍的Pagerank？没错，Pagerank里一个网页的score正比于其连接的其他网页的score的和，这与上面的公式表述的含义正好相同。
(f)Bonacich Centrality: 课程中最后介绍的一种度量中心集中度的方法叫做Bonacich Centrality，定义如下：
\[C^b(g) = ag\mathbf{1}+bgag\mathbf{1}+b^2g^2ag\mathbf{1}\cdots\]取个极限得：
\[C^b(g) = a(g\mathbf{1}+bg^2\mathbf{1}+b^2g^3\mathbf{1}) = (\mathbf{1}-bg)^{-1}g\mathbf{1}\]看的实在有点不明白，这里暂时就不说了。
3.Properties of Networks
每个网络都具有一些性质，如果需要表示满足某种性质的所有图，该如何表示？
| 定义 \(G(N)\) 表示所有节点为集合N的网络（注意N是节点集合，而非节点数量）， \(A(N)\) 表示符合某种条件切节点为集合N的所有网络，显然， \(A(N)\) 是 \(G(N)\) 的子集。例如， $$A(N)={g | N_i(g) \text{nonempty for all?i in N}}$$ 表示所有不包含isolated nodes的网络。 |
Monotone Properties: A property A(N) is monotone if g in A(N) and g subset g’ implies g’ in A(N).
4.Thresholds and Phase Transitions
对于一个Monotone Property A(N)，如果存在一个函数t(n)使得下面两个条件满足，则称t(n)为一个threshold function：
-
Pr[A(N) p(n) ] ‐> 1 if p(n)/t(n) ‐> infinity -
Pr[A(N) p(n) ] ‐> 0 if p(n)/t(n) ‐>0
这里的网络是ER图G(n, p)，即节点数为n，任意一条边存在概率为p，上面两个条件的含义其实就是：如果p比t(n)的数量级要高，则该网络一定属于A(N)；如果p比t(n)的数量级要低，则该网络一定不属于A(N)。
因此，t(n)实际上是网络具备某种性质的一个阈值，p与t的相对大小决定了网络是否满足该性质，下面是由此得到的一些结论：
- \(1/n^2\) ‐ the network has some links (avg deg 1/n)
- \(1/n^{\frac{3}{2} }\) – the network has a component with at least three links (avg deg 1/n^{1/2} )
- 1/n – the network has a cycle, the network has a unique giant component: a component with at least na nodes some fixed a<1; (avg deg 1)
- \(\log{(n)}/n\) ‐ the network is connected; (avg deg \(\log{n}\) )
也就是说当n足够大的时候，如果p的数量级达到 \(\frac{1}{n^2}\) ，那么这个网络不会没有边；如果p的数量级达到 \(1/n^{\frac{3}{2} }\) ，那么该网络包含一个至少三条边构成的连通分量；如果p的数量级达到1/n，那么这个网络很有可能包含环，同时会包含一个唯一的巨大连通分量；如果p的数量级达到 \(\log{(n)}/n\) ，那么这个网络将会是连通的。
