课程已经完结，真是拖延症，这个笔记还没做完，罪过～～赶紧抓紧补完……

上一节课的内容是扩散，比较适合简单的传染病传播建模，然后这一节课的主题有一点不同，尽管也属于某种扩散，但由于整个网络中所有结点具有决策能力，因此不再是简单的概率随机扩散。

1.Bayesian Learning

假设在一个大小为n的无向连通分量（undirected component）里，每个结点单位在每单位时间内可以进行一次决策，选择执行A或者B，对于这两个选择，A会带来1的收益(payoff)，B则可能有概率p带来收益2或者概率1-p带来收益0；每单位时间内每个结点都根据其决策结果获得对应的收益，同时还会关注所有其他邻居的选择，并且所有结点都并不知道p到底是多大，他们的共同目的是使自己在整个时间流上的收益和最大。

显然，如果p是已知的，我们只需要比较p和 \(\frac{1}{2}\) 的关系就能知道应该做出什么选择，但因为p未知，因此每个结点都需要观察邻居结点的行为来判断p可能的大小是多少，然后再做出相应的决定。

课程对于这一问题首先提出了一个命题：只要p不是正好等于 \(\frac{1}{2}\) ，那么在未来某一时刻，网络中所有结点最终将会做出相同的选择（A或B），证明比较简单，如下：

• 假设相反的情况，一部分结点一直选择A，其余结点选择B；
• 根据大数定律，后一部分结点将会最终得到一个非常非常接近真实值的p，而这个值一定大于0.5 ，否则他们应该已经改变选择了；
• 另一方面，所有与那些一直选择B的结点相连的结点最终也会选择B，因为他们看到其他结点一直选择B，就会知道这些结点计算出的p应该是比较接近真实值的；
• 于是所有结点都最终选择了B。

等等，上面这个命题似乎只是说最终所有结点会做出相同的选择，但是并没有提到这个选择是否正确，即是否把收益最大化了。

首先假设p< \(\frac{1}{2}\) ，类似于上面的证明，可以得出即使有一些结点一开始选择了B，但是根据大数定律，最终这些结点一定会发现p应该是小于 \(\frac{1}{2}\) 的，进而导致其邻居结点也最终选择A；再假设p> \(\frac{1}{2}\) ，那么问题来了，如果有一些结点比较顽固，初始就比较相信应该选择A，需要很长的时间才能被其他结点说服去选择B，这时候如果运气好他周围有足够的初始选择B的结点，那么整个网络可能最终一起选择B，但如果没有的话，后果就可能会是整个网络一起选择了A，即做出了一个错误的判断。

2.DeGroot Model

考虑了不包含太多网络结构的简单情况，再考虑一下稍微复杂一些的情况，假设某个网络中有n个结点，T是权重矩阵，其中元素 \(T_{ij}\) 表示i在参考j结点所做选择时的权重，如果每个结点初始对p的估计为 \(b_i(0)\in[0,1]\) ，那么t时刻有 \(b_i(t)=\sum_jT_{ij}b_j(t-1)\) ，好吧，这个熟悉的概率传播公式又出来了，Markov process真是无所不在无所不能……

接下来又是对 \(b_i(t)\) 收敛的分析，不过很有趣，之前我们讨论 \(T^t\) 是否收敛时是根据Perron-Frobenius定律，如果 \(T>0\) 并且T是Primitive的，则无论 \(b_i(0)\) 等于多少，最终都会收敛，不过这回slides中介绍了一个奇特（怪）的方法：

T is aperiodic if the greatest common divisor of its cycle lengths is one

这里所说的cycle lengths实际上是根据传播矩阵T画出的概率传播图中所有环的长度，如果这些cycle lengths最大公约数为1，则T是aperiodic的，意味着 \(T^t\) 是收敛的

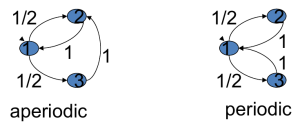至今也不太明白这个aperiodic和Perron定律是个什么联系，o(╯□╰)o

另外，由于这个Markov过程最终稳态其实就是T的特征值为1对应的特征向量，因此每个结点的influence就正好对应了其eigenvector centrality