课程已经过半,社交网络的一些基础概念也已经在前面几节课中介绍了很多,幸运的是虽然后面的内容算是进阶性的,但是难度还好不是特别大。本次课程主要内容只包括一个单词”Diffusion”,即扩散,其在现实世界中可以作为很多不同现象的背后依据。
1.Bass Model
首先介绍的是一个比较简单的扩散模型,注意,这是一个no network model,也就是不包含任何网络结构的模型:Bass Model。
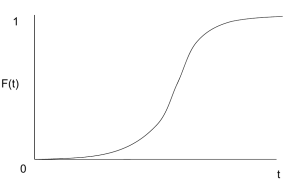
假设现在有一群人(内部没有显示的社会结构),里面所有人都需要做出一项决定,用0和1表示决定的结果, \(F(t)\) 表示t时刻人群中采取决定1的人的比例,并且有两个因素主要影响着 \(F(t)\) :
那么 \(F(t)\) 的变化速率为 \(dF(t)/dt = (p+F(t)q)(1-F(t))\) ,解这个微分方程可以得到:
\[F(t) = \frac{1-e^{-(p+q)t} }{1+qe^{-(p+q)t}/p}\]注意,所有采取决定1的人不会随着时间推移改变成决定0,而采取决定0的人可能会改变为1,上面p表示的是:在之前采取决定0的人群中,每个人有p概率随机改变决定0成1;q表示的是:在之前采取决定0的人群中,他们可能会观察有多少人采取了决定1,并决定他们是不是要改变之前的决定。
如果在q>p时我们把 \(F(t)\) 的曲线画出来可以发现它的形状是一个“S”,即 \(F(t)\) 初始从0开始不断增长,一开始的时候变化缓慢,中间变化迅速,最后又变化缓慢,斜率逐渐归为0。例如当t->0时, \(F(t)\rightarrow 0\) , \(dF(t)/dt\rightarrow p\) ;当 \(F(t)\rightarrow 1\) 时, \(dF(t)/dt\rightarrow 0\) 。前提条件q>p是为了满足在t很小时 \(F(t)\) 的convexity。
2.Bring in interaction structure
刚才的Bass Model是一种最简单的不包含任何内部网络结构的模型,下面我们引入一些简单的结构信息,以一个传染病为应用场景建立新的模型。
- Reach of contagion is determined by the component structure
- Some players or nodes are immune, Some links fail to transmit ...
即传染过程必须满足两个结点之间有连接(接触),而且有一些结点具有免疫性,或者某些连接无法传播。
下面再以Erdos‐Renyi网络为例进行实际分析,首先,ER图的p应该满足 \(1/n<p<log(n)/n\) ,否则整个网络要么全是孤点要么全部连通,只存在一个连通分量。假设q为网络中最大连通分量包含结点数占所有结点的比例,显然任意一个结点在这个连通分量里的概率是q,不在这个连通分量里的概率是1-q;又因为任意一个结点不属于网络最大连通分量的条件是其所有邻居也同样不属于该连通分量,因此有如下等式:
\[1-q = \sum(1-q)^dP(d)\]其中d是该结点的度数,P(d)是结点度数为d的概率,当P(d)满足泊松分布即
\[P(d)=[(n-1)^d/d!] p^d e^{-(n-1)p}\]时,联立两式可得
\[1-q = e^{-(n-1)p}\sum[(1-q)(n-1)p]^d/d!\]联想 \(e^x\) 的泰勒展开 \(e^x = \sum x^d/d!\) ,可以化简上式为:
\[1-q = e^{-pq(n-1)}\]或者
\[E(d) = (n-1)p = -log(1-q)/q\]一个结点属于最大连通分量的概率可以表示为 \(1-(1-q)^d\) ,即任意一个邻居属于该连通分量就可以,显然这个概率随着d增大也增大,这意味着一个结点度数越大,则越容易被传染(好吧,听起来有点像废话)。
如果要处理带有免疫特性的结点,方法很简单,直接把这类结点从网络删除即可。
3.Extensions
继续前一节的例子,在此基础上再进行一些拓展,假设每个结点有概率 \(\pi\) 对该传染病免疫,网络各个结点之间的连接(边)仅有f(百分比)可以进行传染,对这个新的网络进行建模,我们可以通过删除百分比为 \(\pi\) 的结点和1-f的边,然后回到传统模型上来进行模拟。
在进行结点和边的随机删除步骤之后,最大连通分量的结点数占原来所有结点数量的比例为 \(q(1-\pi)\) ,即某个结点可能进行nontrivial contagion的概率是 \(q(1-\pi)\) ,但是占现在结点数的比例仍为q,因此新的网络满足:
\[-log(1-q)/q = (n-1)p(1-\pi)f\]等式右边是新的 \(E(d)\) (原来 \((n-1)p\) 的基础上乘以剩余结点概率 \((1-\pi)\) 和保留边的概率f),根据这个等式,如果 \(\pi\) 足够高或者f、p足够低,传染过程就能停止。
4.SIS Model
既然考虑了某些结点免疫和某些边不能传播,那么还可以加入未感染结点被其他结点感染的概率,以及其自发康复的概率。
那么随着时间推移,最终整个网络可能达到一个稳态,即被感染结点的比例保持不变, \(d\rho /dt = 0\) ,展开左式:
\[d\rho /dt = (1-\rho)(v\rho+\epsilon)-\rho\delta=0\]求解微分方程得到:
\[\rho = [(v-\delta-\epsilon)+((v-\delta-\epsilon)^2+4\epsilon v)^{1/2}]/2v\]如果在此基础上简化一下模型,比如令 \(\epsilon=0\) ,则可以得到
\[\rho = 1-\delta/v \text{ if > 0}\] \[\rho=0\]这里含义很明显,若 \(\delta>v\) ,则表示康复的速度比感染速度快,因此最终所有结点都会康复,否则, \(\rho\) 会保持在某一个恒定的数值。
等等,我们好像又把网络结构给忽略了,如果任意一个结点在单位时间内和 \(d_i\) 个其他结点有接触,用 \(\rho(d)\) 表示度数为d的结点被感染的概率, \(\theta\) 表示随机接触的邻居被感染的比例, \(P(d)\) 表示某结点在单位时间内度数为d的概率,那么
\[\theta = \sum\rho(d)P(d)d/E[d]\]当网络达到稳态,有
\[d\rho(d)/dt = (1-\rho(d))v\theta d-\rho(d)\delta\]右边第一项表示尚未感染结点自发病变,而第二项表示已感染结点自发康复。求解上式得:
\[\rho(d) = \lambda\theta d/(\lambda\theta d+1), \text{ where } \lambda=v/\delta\]